La Palma, Canary Islands, Spain –Between January and February 2020, the prototype Large-Sized Telescope (LST), the LST-1, observed the Crab Pulsar, the neutron star at the centre of the Crab Nebula. The telescope, which is being commissioned on the CTA-North site on the island of La Palma in the Canary Islands, was conducting engineering runs to verify the telescope performance and adjust operating parameters.

Pulsars are very rapid rotating and strongly magnetized neutron stars that emit light in the form of two beams, which can be observed from Earth only when passing our line of sight. While detecting the strong and steady emission or outbursts of gamma-ray sources with Imaging Atmospheric Cherenkov Telescopes (IACTs) has become routine, pulsars are much more challenging to detect due to their weak signals and the typical dominance of the foreground gamma-ray signal from the surrounding nebulae. Despite hundreds of observations hours by IACTs around the globe, only four pulsars emitting signals in the very high-energy gamma-ray regime have been discovered, so far. Now that the LST-1 has shown that it can detect the Crab pulsar, it joins the field of telescopes capable of detecting gamma-ray pulsars, validating the timestamping system and the low-energy performance of the telescope.
“This milestone shows us that the LST-1 is already performing at an extraordinary level, detecting a challenging source in record time,” says Masahiro Teshima, Director of Max-Planck-Institute for physics in Munich and Principal Investigator of LST. “Pulsars are one of the key scientific targets of the LSTs, and it’s exciting to imagine what we’ll be able to achieve when the telescope is fully commissioned and operational.”
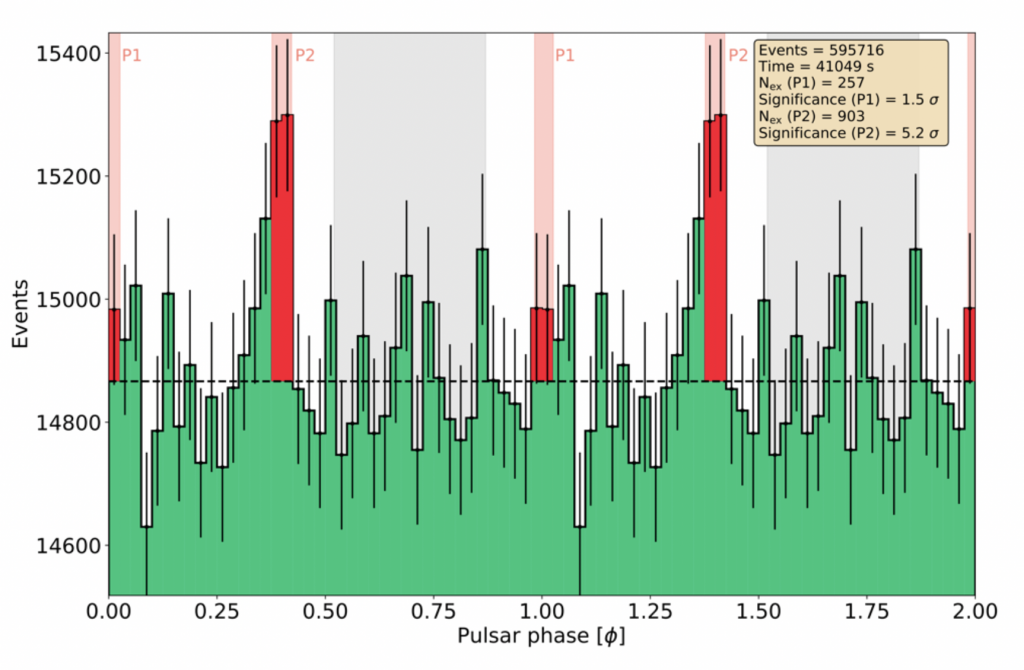
The data set collected includes 11.4 hours from eight observation nights. Figure2 shows the resulting phasogram, plotting the gamma-ray events as a function of the pulsar rotation phase. The flat background is a mixture of gamma-like isotropic cosmic rays and dominant irreducible steady emission from the Crab pulsar wind nebula. In the phase regions marked P1 and P2, one expects to see more gamma rays in these time intervals as gamma rays from the Crab pulsar are emitted towards the Earth. The signal detected with the LST-1 is undeniably significant for phase P2, while the signal during P1 is still marginal. The animation in Figure3 highlights the pulse behavior of the source during the different phases.
About the LST
The Large-Sized Telescope (LST) is one of three types of telescope to be built to cover CTA’s full energy range (20 GeV to 300 TeV). LSTs arranged at the centre of both the northern and southern hemisphere arrays will cover the low-energy sensitivity between 20 and 150 GeV. Each LST is a giant 23 metre diameter telescope with a mirror area of about 400 square meters and a fine pixelized camera made of 1855 light sensors capable of detecting individual photons with high efficiency. Although the LST stands 45 metres tall and weighs around 100 tonnes, it is extremely nimble, with the ability to re-position within 20 seconds to capture brief, low-energy gamma-ray signals. Both the fast re-positioning speed and the low energy threshold provided by the LSTs are critical for CTA’s studies of transient gamma-ray sources in our own Galaxy and for the study of active galactic nuclei and gamma-ray bursts at high redshift.
The LST collaboration, consists of more than 200 scientists from 11 countries: Brazil, Bulgaria, Croatia, France, Germany, India, Italy, Japan, Poland, Spain and Switzerland. The LST-1, the first telescope constructed on a CTA site, was inaugurated in October 2018 and has been undergoing commissioning testing ever since. Soon after the inauguration, the prototype detected its ‘first light’ on the evening of 14-15 December, and it detected its first gamma-ray signal from the Crab Nebula in November 2019 on its first attempt.
The LST-1 recently passed the Critical Design Review (CDR) by the CTA Observatory (CTAO), the first CTA element to pass such a review. The telescope is foreseen to become the first CTAO telescope once the CDR is closed out and it is formally accepted by the CTAO, which is expected in 2021.
About CTA
The Cherenkov Telescope Array (CTA) is a global initiative to build the world’s largest and most sensitive high-energy gamma-ray observatory with tens of telescopes planned on two sites: one in the northern hemisphere on the island of La Palma, Spain, and the other in the southern hemisphere near Paranal, Chile. CTA will be the foremost global observatory for very high-energy gamma-ray astronomy over the next decade and beyond and will be the first ground-based gamma-ray astronomy observatory open to the world-wide astronomical and particle physics communities. CTA will address some of the greatest mysteries in astrophysics, detecting gamma rays with an unprecedented sensitivity and expanding the cosmic source catalogue tenfold. CTA is a unique, ambitious large-scale infrastructure that will expand observations up to a region of the spectrum that has never been seen, opening an entirely new window to our Universe. The CTAO gGmbH serves to prepare the design and implementation of the CTA Observatory. The CTAO works in close cooperation with the CTA Consortium composed of 1500+ members from 31 countries, which is responsible for directing the science goals of the Observatory and is involved in the design and supply of instrumentation. The CTAO is governed by a council of shareholders from 11 countries and one intergovernmental organization, as well as associate members from two countries.
Contacts:
Masahiro Teshima
LST Principal Investigator
MPP Munich and ICRR University of Tokyo
mteshima@mpp.mpg.de
Juan Cortina
LST Co-Principal Investigator
CIEMAT, Madrid
cortina@ciemat.es
Daniel Mazin
LST Project Manager
ICRR University of Tokyo and MPP Munich
mazin@icrr.u-tokyo.ac.jp
Megan Grunewald
Outreach and Communications Officer
CTAO gGmbH
mgrunewald@cta-observatory.org







